Rule Set Analyser module

Structures

The following structures are used by the analyzer for checking some rule classes. Furthermore, the graph of rule dependencies is also used in the combination step to define rule subsets (which correspond to its strongly connected components).

Frontier of a rule

The frontier of a rule is the set of variables that occur both in the body and the head of the rule. These variables are called frontier variables.

Graph of rule dependencies

The graph of rule dependencies (GRD) is a directed graph built from a rule set as follows: there is a vertex for each rule in the set and there is an edge from a rule R₁ to a rule R₂ if R₂ depends on R₁, i.e., there is a fact base such that an application of R₁ may lead to trigger a new application of R₂ that effectively adds new atoms (this application is said to be productive). For advanced users: R₂ depends on R₁ if and only if there is a piece-unifier of the body of R₂ with the head of R₁ which is (1) atom-erasing and (2) productive.
For the notion of atom-erasing piece-unifier, see f.i. this paper. Note that for efficiency reasons, Kiabora computes a weaker version of the atom-erasing test: given a piece unifier u, it simply checks that u(Body(R₂))) is not included in u(Body(R₁))).
The productivity condition for a piece-unifier u expresses that u(Head(R₂)) is not included in u(Body(R₁)) U u(Head(R₁)) U u(Body(R₂)).

Graph of restricted rule dependencies (GRRD)

In the previous GRD, a rule application is said to be productive if it adds at least one new atom to the fact base. This corresponds to the notion of rule application performed by the simple forward chaining known as oblivious chase. The forward chaining known as restricted chase does not perform a rule application if the atoms that would be added can be `folded' into the existing fact base (hence, it detects a form of local redundancy). The graph of restricted rule dependencies (GRRD) enforces a stronger productivity condition so that there is a new application of R₂ according to the restricted chase. Hence, the GRRD may have less dependency edges than the GRD.

Graph of Predicate Positions

In this graph, a vertex (hence a predicate position) is of finite rank if there is no circuit containing a special edge and passing through this vertex.

Marked Variable Set

The marked variable set is built from a rule set by the following marking procedure:
(i) for each rule R_i and for each variable v occurring in the body of R_i, if v does not occur in all atoms of the head of R_i, mark (each occurrence of) v in the body of R_i;
(ii) apply until a fixpoint is reached: for each rule R_i, if a marked variable v appears at position p[k] in the body of R_i, then for each rule R_j (including i = j) and for each variable x appearing at position p[k] in the head of R_j, mark each occurence of x in the body of R_j.

Affected Position Set

A position p[i] is affected if (1) there is an existential variable occurring in position p[i] in the head of a rule, or (2) there is a frontier variable that occurs both in position p[i] in the head of a rule R and in an affected position in the body of R.

A variable from a rule body is said to be affected if it occurs in some affected position.

The affected position set of a rule set is the set of all its affected positions.

Jointly-Affected Position Set

The jointly-affected position set is built from a rule set by the following procedure:
(i) for each rule and for each existentially quantified variable occuring at position p[i] in its head, p[i] is jointly-affected;
(ii) for each rule and for each variable x that occurs only at jointly-affected positions in its body, all positions q[j] in its head where x occurs are jointly-affected.

A variable is said to be jointly-affected if it occurs only at jointly-affected positions.

Rule Classes

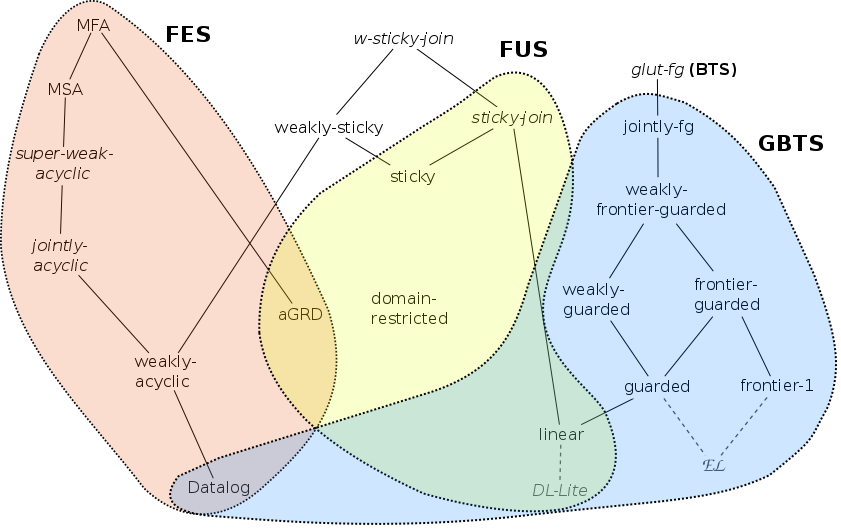The rule classes are divided into two types: abstract classes, which ensure decidability of conjunctive query answering but are not recognizable, i.e., one cannot always determine if a set of rules belongs to such a class, and concrete classes, which may specialize one or several abstract classes and are recognizable by syntactic properties.

In the figure on the right side, rule classes are ordered by inclusion: an upwards edge from class C1 to class C2 means that C1 is included in C2. If there is no edge between two classes, it means there are incomparable. Note that a class was omitted in this picture for the sake of readability: disconnected rules, which are fes, fus and gbts, and are a specialization of domain-restricted, weakly-acyclic and frontier-guarded rules.

For information, the well-known description logics DL-Lite_R and EL have been included in the picture.

The concrete classes mentioned in italics in the figure are not considered yet by the analyzer, hence they are not described below. These classes are the following:

• super-weak-acyclic
• jointly-acyclic
• sticky-join
• weakly-sticky-join (w-sticky-join)
• glut-fg

Abstract Rule Classes

These rule classes are called abstract because they are not characterized by a syntactic property. They are used to classify concrete classes. Each of these classes ensures the existence of query mechanisms that halt in finite time for any (conjunctive) query and any set of facts. In general, determining if a rule (or a set of rules) belongs to one of these abstract classes is known to be undecidable, except for gbts for which the question is open.

Finite expansion set (fes)

This abstract class ensures the finiteness of any forward chaining algorithm that saturates the facts until fixpoint with respect to logical equivalence. Hence, query answering can be solved by mapping the query to the saturated facts.

Finite unification set (fus)

This abstract class ensures the finiteness of any backward chaining algorithm that rewrites the query in a breadth-first manner while maintaining a set of the most general rewritings. This class is also called UCQ-rewritable (and known to be equivalent to first-order rewritable) Query answering can be solved by rewriting the initial query then mapping the rewritten query to the facts.

(Greedy) Bounded treewidth set (bts)

The BTS class, which strictly includes FES, ensures decidability, although there is currently no algorithm available for this class. However, Greedy Bounded Treewidth Set (GBTS) is an expressive subclass of BTS that is provided with a forward-chaining-like halting algorithm. Almost all currently known BTS but not FES classes are GBTS.

Concrete Rule Classes

These classes are presented with their syntactic properties and the abstract classes they belong to.

There are two kinds of syntactic properties:

• local properties which are checked on each rule independently from the others (hence a set fulfils a local property if all of its rules fullfil it);
• global properties which are checked on a set of rules (note that the analyzer may partition the input set of rules into subsets corresponding to the strongly connected components of the graph of rule dependencies and check the global properties of each component).

Reminder: the frontier of a rule is the set of variables that occur n both the body and the head of the rule.

Acyclic graph of rule dependencies (agrd)

This rule class property is a global property.
Ensures:

• fes
• fus

The associated graph of rule dependencies has no circuit.

Atomic-body (ab)

Datalog (dlg)

Disconnected (disc)

This rule class property is a local property.
Ensures:

• fes
• fus
• gbts

The frontier is empty. Note that any disconnected rule needs to be applied only once up to logical equivalence.

Domain-restricted (dr)

This rule class property is a local property.
Ensures:

• fus

Each atom in the head contains all variables from the body or none.

Frontier-guarded (fg)

This rule class property is a local property.
Ensures:

• gbts

At least one atom in the body contains all the variables from the frontier.

Frontier-one (fr1)

This rule class property is a local property.
Ensures:

• gbts

The frontier contains only one variable.

Guarded (g)

This rule class property is a local property.
Ensures:

• gbts

At least one atom in the body (called a guard) contains all the variables from the body.

Jointly-frontier-guarded (jfg)

This rule class property is a global property.
Ensures:

• gbts

At least one atom in the body of each rule contains all jointly-affected variables from the frontier (cf. jointly-affected position set).

Linear (lin)

This rule class property is a local property.
Ensures:

• fus
• gbts

The body contains a single atom.

Model-faithful acyclicity (mfa)

This rule class property is a global property.
Ensures:

• fes
• bts

The skolem chase executed on the critical instance does not produce any 'cycle of functional symbols'.

Model-summarising acyclicity (msa)

This rule class property is a global property.
Ensures:

• fes
• bts
• mfa

Approximates MFA with a lower complexity.

Range-restricted - or Datalog (rr)

This rule class property is a local property.
Ensures:

• fes
• gbts

All variables that appear in the head also occur in the body.

Sticky (s)

This rule class property is a global property.
Ensures:

• fus

Each marked variable occurs at most once in a rule body (cf. marked variable set).

Weakly-acyclic (wa)

This rule class property is a global property.
Ensures:

• fes

All predicate positions in the graph of predicate positions have finite rank (i.e., there is no circuit with a special edge).

Weakly-frontier-guarded (wfg)

This rule class property is a global property.
Ensures:

• gbts

At least one atom in the body of each rule contains all the affected variables from the frontier (cf. affected position set).

Weakly-guarded (wg)

This rule class property is a global property.
Ensures:

• gbts

At least one atom in the body of each rule contains all the affected variables from the body (cf. affected position set).

Weakly-sticky (ws)

This rule class property is a global property.
Ensures:

This class does not belong to any abstract class defined earlier. It is a generalisation of Sticky and Weakly-Acyclic. It relies upon the same graph of predicate positions as the Weakly-Acyclic test and upon the same marking procedure as the Sticky test. All marked variables that occur more than once in a rule body appear at some position of finite rank.